In questo articolo vedremo l’equazione di De Moivre, uno strumento statistico fondamentale per il monitoraggio in tempo reale di sport, politica e frodi finanziarie. Cercheremo inoltre di capire come Isaac Newton abbia commesso il suo più grande errore matematico durante il suo soggiorno alla Zecca Reale. Questo articolo è tratto da un capitolo del fantastico libro “Numeri Intelligenti” di Nicholas Polson e James Scott. Se finita la lettura di questo sunto correrai a comprare il libro potrò dire di aver raggiunto l’obiettivo!
Table of Contents
- L’Inghilterra e la sterlina
- La Prova della Pisside
- L’Equazione di De Moivre
- Entriamo Nella Formula
- L’arrivo di Newton
- Le Frodi Ieri…
- … E Oggi!
- Conclusioni
L’Inghilterra e la sterlina
Se Isaac Newton è universalmente riconosciuto come uno dei più grandi scienziati della storia grazie alle sue leggi di gravitazione, l’invenzione del calcolo infinitesimale e gli studi sulla natura della luce, in pochi sanno che ha ricoperto anche il ruolo di direttore della Zecca Reale inglese.
Prima di introdurci nei dettagli del suo operato, immergiamoci brevemente nella realtà storico-economica in cui la nostra storia si svolge.
L’Inghilterra del XVII secolo utilizzava lo standard monetario in argento e nel 1696, anno in cui Newton arrivò alla Zecca, la moneta inglese scarseggiava ormai da almeno trent’anni. I motivi sono presto detti: in primis, a causa della guerra dei nove anni, la richiesta di argento dall’Europa Continentale era talmente alta da convincere gli intraprendenti inglesi a esportare le sterline in Francia o in Olanda, fonderle, permutare l’argento grezzo in oro e rivenderlo, piuttosto che utilizzarle nel proprio paese come mezzo di pagamento.
La Limatura
La seconda causa di scarsità della valuta va cercata, invece, nella poco nobile pratica della limatura. Quando una moneta aveva una sporgenza di troppo e la quantità di argento era superiore al livello “standard”, ci si adoperava ad asportare con cura la parte in eccesso. Se da un singolo scellino si otteneva ben poco, da una gran massa di monete si poteva accumulare una notevole quantità d’argento. Il costo della limatura poteva essere però decisamente alto visto che la condanna era l’impiccagione!
Fino al 1662 la limatura era agevolata dal fatto che le monete erano realizzate a mano da fabbri che battevano un blocco d’argento su un’incudine fino a trasformarlo in un disco piatto. Dunque, la forte variabilità tra i vari dischi era una caratteristica comune delle monete.
Per risolvere il problema il Parlamento si prodigò a fornire i fondi necessari alla produzione meccanica delle sterline, così da avere una produzione standardizzata che rendesse minima la variabilità del peso e della forma dei dischi d’argento.
Il problema, dopo trent’anni, fu dunque risolto? No. E per questo motivo: le monete vecchie, costruite a mano, erano ancora in circolazione ed accettate al loro valore nominale. Perciò erano queste a venir messe in circolazione e non quelle di miglior fattura, esportate e fuse sul continente.
La Prova della Pisside
Per verificare che non ci fossero eccessive anomalie nella produzione di sterline, sin dal 1150 ci si affidava alla cosiddetta “Prova della Pisside”. Questa procedura consentiva di verificare l’onestà della Zecca e la sua capacità nel “controllo qualità” della produzione di moneta. Si procedeva così: ogni sessanta libbre di argento veniva messa da parte una sterlina. Dopo averne accumulato diverse migliaia (in qualche anno) dei fabbri scelti verificavano eventuali anomalie. Perché accumulare un tale quantitativo di sterline e pesare migliaia di monete insieme? Semplicemente perché era un processo più veloce rispetto alla misura di ogni singola sterlina, ancorché in un campione finito ma comunque molto numeroso.
Sottolineiamo che la variabilità delle monete costruite manualmente era inevitabile. Proprio per questo motivo la legge inglese permetteva che ciascuna sterlina differisse dal valore di riferimento per un ammontare pari al massimo all’1%1, in eccesso o in difetto.
L’Equazione di De Moivre
La domanda fondamentale da porsi è però la seguente: “se una moneta può avere un peso che varia di ±1%, di quanto è autorizzato a variare il peso medio di un campione di monete? “
La risposta che sembrava ovvia ai legislatori inglesi era l’1%. Ma questa è, come il lettore avrà intuito, errata.
Ad aiutarci entra in gioco l’equazione di De Moivre, detta anche “regola della radice quadrata”, prodigiosa scoperta del matematico svizzero Abraham De Moivre. Questa equazione è fondamentale sia in statistica che nel campo dell’intelligenza artificiale. Essa stabilisce, come vedremo in dettaglio, la relazione esistente tra la variabilità di un campione e la radice quadrata della numerosità dello stesso. Gli ufficiali della Zecca avrebbero avuto un grande all’alleato per individuare anomalie durante la prova della Pisside!
Ecco la formula matematica:
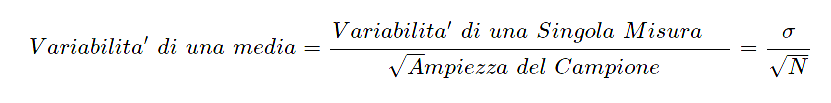
Entriamo Nella Formula
Facciamo un esempio numerico per meglio intuire la profondità dell’equazione di De Moivre. Se la variabilità massima concessa ad una singola sterlina (che ipotizziamo ad esempio di 100 grammi) è pari a 1 grammo, quella permessa ad un campione di 2500 sterline dovrà essere di 0,02 g (1/√2500) e non di 25 grammi come si pensava. L’errore è notevole: è più di tre ordini di grandezza!
Studiamo l’equazione di De Moivre anche per intervalli diversi:
| Ampiezza del campione | Limiti usati nella Prova della Pisside | Limiti corretti basati sulla statistica moderna |
| 1 | 100 ± 1,00 | 100 ± 1,00 |
| 100 | 100 ± 1,00 | 100 ± 0,10 |
| 2500 | 100 ± 1,00 | 100 ± 0,02 |
| 10000 | 100 ± 1,00 | 100 ± 0,01 |
Da dove nascono dunque queste differenze così marcate? Le differenze derivano dal fatto che in un campione numeroso le sterline che superano i 100 grammi si “annullano” con quelle dal valore inferiore. In un grande campione una moneta leggera può essere controbilanciata da una pesante, mentre in un campione piccolo la moneta leggera può abbassare la media.
Questo errore matematico lascia alcuni spunti di riflessioni. Il primo, anche se molto improbabile, è che gli stessi dipendenti della Zecca avrebbero potuto limare le sterline. Perché? limando mezzo grammo da ogni sterlina prodotta in Inghilterra si era comunque all’interno dei limiti legali! E’ molto probabile invece che la produzione e il controllo qualità fossero semplicemente negligenti provocando un notevole danno all’economia inglese. In conclusione, se i valori si allontanano dai valori stabiliti dall’equazione di De Moivre, i sospetti di una truffa o di una pessima produzione dovrebbero decisamente salire.
L’arrivo di Newton
Come abbiamo anticipato Newton entrò nella Zecca Reale nel 1696 accorgendosi subito che gli standard di produzione manuale erano molto deficitari. Dobbiamo anche ricordare che lo scienziato inglese arrivò in un momento decisivo, ossia durante la grande coniazione di monete, in cui milioni di sterline prodotte a mano furono richiamate, fuse e riforgiate a macchina. Poiché la velocità di produzione meccanizzata andava ad una velocità di circa 3 o 4 sterline al minuto, era impossibile ultimare il lavoro entro tempi accettabili. Newton allora si adoperò per migliorare il sistema di coniazione come un moderno ingegnerie di produzione, ottimizzando il processo a tal punto da poter produrre 50 monete al minuto, dalle quattro del mattino alla mezzanotte, sette giorni su sette, per due anni.
Ovviamente le monete da lui prodotte passarono l’esame della pisside con dei limiti così poco stringenti. Risulta però incredibile pensare che nonostante Newton sia stato una delle menti più brillanti della storia umana, non si sia mai posto la seguente domanda: “com’è possibile che monete così mal prodotte, di peso e forma così variabili, siano riuscite a superare l’esame della pisside per secoli? L’equazione di De Moivre non poteva essere scoperta prima da Newton, così da diventare la sua di equazione? Ai posteri l’ardua sentenza…
Le Frodi Ieri…
Nella nostra moderna economia digitale ciò che spaventa di più banche e clienti di tutto il mondo sono le frodi informatiche.
Eppure, truffe e raggiri sono antichi come il mondo, specie quelle che coinvolgono bilance. E’ ben nota la storia della calata dei Galli e del Sacco di Roma del 390 A.C. Eccone un breve resoconto. Dopo un estenuante assedio sul Campidoglio i Romani sono disposti a trattare la resa con i nemici che assicurano un riscatto non esorbitante. Il Senato invia per le trattative il tribuno Quinto Sulpicio mentre per i Galli c’è il loro capo in persona, Brenno. La richiesta per lasciare l’assedio è di mille libbre d’oro, ossia 327 kg! Oltre alla vergogna viene aggiunto l’oltraggio: i Galli portano dei pesi falsi e alle proteste del tribuno, il Gallo Brenno getta con arroganza sulla bilancia la propria spada pronunciando: “Vae Victis!” (“Guai ai Vinti!”).
Ma ecco dunque che arriva Camillo, il comandante dei Romani, che rinnega i patti, stipulati senza il suo consenso, incita i suoi concittadini a “riscattare Roma con il ferro e non con l’oro” e sconfigge i nemici in battaglia, salvando la Patria.
… E Oggi!
Se in passato la lotta alla frode era affidata all’intelligenza e al controllo umano, oggi risulterebbe impossibile vigilare sulle migliaia di miliardi di transazioni digitali.
Anche l’intelligenza artificiale però, fino a pochi anni fa, non era in grado di operare abbastanza velocemente su database enormi per trovare anomalie in tempo reale. Per questo motivo ci si accontentava di rilevare anomalie basate su semplici regole, come luogo, data e ammontare della transazione. Oppure, se si voleva avere un maggior numero di dettagli conservati nei database bisognava attendere mesi e non millisecondi!
PayPal oggigiorno è una delle aziende ad aver risolto il problema dell’eccessiva ampiezza e contestuale profondità dei database. L’azienda fondata da Peter Thiel e soci rileva le frodi con un sistema di deep learning per confrontare ogni transazione con gli storici precedenti e il comportamento di altri individui simili, calcolando una probabilità di transizione fraudolenta usata per accettare o rifiutare il pagamento. Tutto in una frazione di secondo.
Conclusioni
Con questo articolo abbiamo scoperto come una “semplice” equazione possa aiutarci a scovare anomalie in vasti insiemi di dati. L’equazione di De Moivre associa la variabilità di un elemento in un campione alla numerosità dello stesso per scovare la corretta variabilità da attribuire al campione nel suo insieme. Se l’equazione della “radice quadrata” fosse stata scoperta molto prima del XVIII secolo, la Zecca Reale Inglese non avrebbe eseguito test di controllo in modo fallace per secoli. In ogni caso oggigiorno la scoperta di De Moivre è ampiamente utilizzata e ci protegge in tempo reale da truffe, frodi e pessimi controlli qualità.
Ah, un’ultima nota: la prova della Pisside si svolge ancora oggi. Anche se le sterline non sono più in argento, una commissione di orafi si riunisce a Londra per pesare e valutare la loro qualità, senza però commettere gli errori del passato!
Se ti è piaciuto questo articolo potresti apprezzare anche: “Il Teorema di Bayes: la Formula per Prevedere il Futuro“
Bibliografia: Numeri Intelligenti, Nick Polson & James Scott, Utet, 2016.
- In realtà era dello 0,7% ↩︎